Các đơn vị cơ bản sử dụng trong kiểm tra độ rung
Có bốn đơn vị quan trọng, lực (N) gia tốc (m/s2) tốc độ (m/s) và độ dịch chuyển (biên độ) (mm đỉnh tới đỉnh)
| F = mA | Đơn vị SI | Đơn vị trọng trường | |
| F : force | N | Kgf | |
| m : mass | Kg | Kg | |
| A : acceleration | m/S2 | G |
Theo đó, nếu vật có khối lượng 1kg gia tốc tới 1m/s2 thì cần một lực 1N. Gia tốc trọng trường G bằng 9.8m/s2
Để mô tả độ rung, tần số và biên độ cần phải xác định. Rung là một dạng của chuyển động, với mối tương quan giữa gia tốc, tốc độ và độ dịch chuyển (biên độ). Để mô tả biên độ rung, mọi đơn vị này đều có thể được sử dụng. Dưới đây là mối tương quan giữa các đơn vị này
Chúng ta có một vật chuyển động theo hình sine
Độ dịch chuyển (quãng đường di chuyển)
D=D0 sinωt
Vận tốc thì bằng đạo hàm của độ dịch chuyển (biên độ). Do đó

Gia tốc thì bằng đạo hàm của vận tốc

Ngoài ra
ω=2πft
Chúng ta có được các hàm với biến là biên độ

Biểu đồ dưới đây thể hiện biên độ, vận tốc và gia tốc
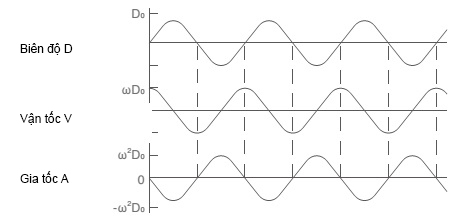
Chúng ta có được các hàm dưới đây bằng cách biến đổi các hàm bên trên

Trong kiểm tra độ rung, chúng ta sử dụng hóa vị đỉnh mm p-p
Do đó

Thay vào tất cả các hàm bên trên

Ví dụ

Chúng ta sử dụng đơn vị dB khi mô tả mối tương quan giữa các đại lượng vật lý. Đặc biệt trong trường hợp khi một giá trị là một bội hàng nghìn hoặc triệu lần của giá trị tương ứng, khi đó chúng ta sử dụng thang logarit thay cho thang tuyến tính. Điều này giúp dễ hình dung các giá trị hơn và là một tiêu chuẩn kiểm tra công nghiệp
dB được diễn tả theo bên dưới:

Một triệu lần bằng

dB không chỉ giảm số lượng số cần dùng mà còn đơn giản hóa phép tính. Ví dụ, 25dB cộng 30dB bằng 55dB nhưng nếu tính theo thang tuyến tính
25dB = 20 log A A = 1025/20=17.78
30dB = 20 log B B = 1030/20=31.62
AxB = 17.78×31.62=562.3=20 log 562.3 = 55dB
Giờ chúng ta có thể sử dụng phép cộng thay cho phép nhân bằng cách sử dụng dB. Hay nói cách khác sử dụng dB rất dễ để tính toán. Dưới đây là bảng chuyển đổi giữa dB và bội số của dB.

Sử dụng đồ thị logarit
Chúng ta thường sử dụng đồ thị logarit khi cần vẽ dữ liệu của kiểm tra độ rung hoặc các hiện tượng vật lý khác
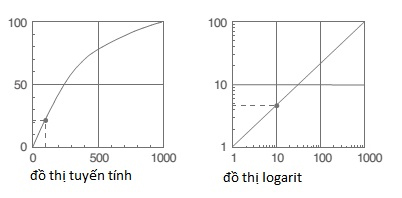
Trên đồ thị tuyến tinh chúng ta có thể xác định Y=20 khi X=100. Nhưng chúng ta khó có thể xác định Y khi X bằng 10 hoặc 1. Trên đồ thị logarit chúng ta có thể xác định giá trị ngay cả khi X là 1/100 hay 1/1000. Do đó sử dụng đồ thị logarit tiện lợi hơn nhiều
Chúng ta thường sử dụng đồ thị bên dưới khi kiểm tra độ rung hình sine. Đây là đồ thị log-log đã được đề cập bên trên. Tiệm cận của gia tốc, vận tốc và hoán vị cố định được thể hiện trên đồ thị. Dưới đây là một ví dụ về tiệm cận của tốc độ không đổi. Từ các hàm chúng ta biết trước

Đẳng thức này cho thấy gia tốc A tăng 100 lần khi tần số f tăng 10 lần. Trên đồ thì bên dưới, chúng ta có thể thấy gia tốc tăng từ 1m/s2 tới 100m/s2 khi tần số tăng từ 1Hz tới 10Hz


Đồ thị thể hiện các tiệm cận khi vậ tốc và hoán vị là bất biến